- 4 blog posts per month - This is still hard, so I'm not increasing it.
- Flash Fiction Friday, the 3rd Friday of each month (with that Saturday as a backup), starting in February - I totally forgot this month, but I had a scheduling conflict, anyway.
- Finish first stage of research into Greek mythology - This means something specific to me, but I'm being vague here.
- Follow my exercise schedule - The schedule itself might change, as needed, but I've got one currently, and so far I'm managing to keep to it.
- Beat Myst again - OK, I forgot last year, but I definitely want to do it this year.
- I'm also hoping to beat at least 1 other game in this series. They're not exactly long, but I've got to get around to doing them.
- Beat Pokémon OR/AS - This means beating the Elite 4, but I have, like, no progress on this so far. -_-
Saturday, January 31, 2015
New Year's Resolutions 2015
I never got around to finalizing my resolution list for this year, so here it is.
On Helping Others Find Sites
I was recently reading yet another article on how a site's livelihood - in this case, MetaFilter's - was threatened because a search engine - in this case, Google - made a secret change to its secret algorithms. Every once in a while, an article like this crosses my path, though I have to wonder how many I don't see because I don't see the tweet, or because nobody in my timeline tweeted or retweeted it because they didn't know about it because it doesn't show up on search engines. Also, even though I said "search engine" twice, this also applies to social networking sites, though in different ways. On the one hand, I'm glad that my livelihood doesn't depend on a website (I'm not even currently running any), but on the other hand, it's because of that that it's easy to forget how big of a deal this is to some people.
I recently tweeted that people should use at least three search engines - unless they can get exactly half of their searches into each of two - and the point of this, really, is to avoid letting anyone get a monopoly. Google has a higher "household name" stat than anyone else. Bing is getting traffic from people too lazy to use anything other than IE. Yahoo is now getting traffic from people comfortable with using FireFox's default engine. Last I checked, Ask.com was still trying to trick people installing Java or Flash or something into changing their browser's default to Ask.com. Even this trickery is understandable, given how much sway Google holds, but even if some other search engine takes the lead, that just changes who the default is. Ever since search engines got good - prioritizing sites by relevance instead of just listing them - our behavior has changed.
Search engines, ads, and social media sites are said to "drive traffic" - or not, as the case may be - to any given site. However, this is sometimes fraught with pitfalls, too, as is the case with facebook. I'll recap, for those who haven't heard: A while ago (last year or the year before, I forget), it was revealed that facebook was sometimes hiding updates by people/groups/pages from people who followed those people/groups/pages, unless those people/groups/pages paid money to make sure that all of their followers got to see it. Of course, since facebook is charging the content creators, most users don't know that stuff is being hidden from them; they're not told that there's a missing update, so they don't know that there's a hole in their timelines. As it happens, just the other day, someone made a comic summarizing this topic again.
People have been communicating with each other over the internet for as long as it has existed - that's kind of the point of it, after all. Social networking sites have been around longer than the name, and even longer than really old ones like friendster, but they were called "forums". Even before that, though, there were instant messaging services, chatrooms, and even Usenet groups. Websites exited, too, once they were invented, but the most common ways that people found out about sites was by being told about them, either by their fellow users (even, believe it or not, offline) or by other sites. (This is back when webrings were still seen on a regular basis.)
I think that we need to make a point of doing this more, as it has waned. That's not to say that we need to sign up for Usenet groups or idle in chatrooms all day, but we should make a point of telling each other about good sites, and asking each other instead of relying on search engines. I don't know exactly the best way to do it, but here are some tips:
I recently tweeted that people should use at least three search engines - unless they can get exactly half of their searches into each of two - and the point of this, really, is to avoid letting anyone get a monopoly. Google has a higher "household name" stat than anyone else. Bing is getting traffic from people too lazy to use anything other than IE. Yahoo is now getting traffic from people comfortable with using FireFox's default engine. Last I checked, Ask.com was still trying to trick people installing Java or Flash or something into changing their browser's default to Ask.com. Even this trickery is understandable, given how much sway Google holds, but even if some other search engine takes the lead, that just changes who the default is. Ever since search engines got good - prioritizing sites by relevance instead of just listing them - our behavior has changed.
Search engines, ads, and social media sites are said to "drive traffic" - or not, as the case may be - to any given site. However, this is sometimes fraught with pitfalls, too, as is the case with facebook. I'll recap, for those who haven't heard: A while ago (last year or the year before, I forget), it was revealed that facebook was sometimes hiding updates by people/groups/pages from people who followed those people/groups/pages, unless those people/groups/pages paid money to make sure that all of their followers got to see it. Of course, since facebook is charging the content creators, most users don't know that stuff is being hidden from them; they're not told that there's a missing update, so they don't know that there's a hole in their timelines. As it happens, just the other day, someone made a comic summarizing this topic again.
People have been communicating with each other over the internet for as long as it has existed - that's kind of the point of it, after all. Social networking sites have been around longer than the name, and even longer than really old ones like friendster, but they were called "forums". Even before that, though, there were instant messaging services, chatrooms, and even Usenet groups. Websites exited, too, once they were invented, but the most common ways that people found out about sites was by being told about them, either by their fellow users (even, believe it or not, offline) or by other sites. (This is back when webrings were still seen on a regular basis.)
I think that we need to make a point of doing this more, as it has waned. That's not to say that we need to sign up for Usenet groups or idle in chatrooms all day, but we should make a point of telling each other about good sites, and asking each other instead of relying on search engines. I don't know exactly the best way to do it, but here are some tips:
- Don't assume that someone interested in a topic already knows about <site>.
- If someone asks you about good sites/the best site for something, don't tell them to <search engine> it.
- Every now and then, <search engine> for <topic>, then skip the first three pages of results, and see if you find any diamonds in the rough. (If you do, then tell people about them.)
- Every now and then, go through your bookmarks and see if there's a site that you haven't visited in a while. If it's still there and still good, then tell people about it.
- It's going to be a very long time before people get weaned off of search engines. Be patient with this.
An Initial Review of Civilization V
Recently, there was a free weekend on Steam for Sid Meier's Civilization: Beyond Earth, and I took a crack at it. I enjoyed it, even though I didn't finish it. However, it occurred to me that I'd never actually played a game in the Civilization series. All of the Civilization titles were 75% off on Steam that weekend, so I went ahead and picked up Sid Meier's Civilization V.
I've finally finished my first game of it.
I really quite enjoyed the game. There's a lot to it, but because of the way that civilizations progress, it's not all dumped out at once. Also, it's turn-based, so I'm not rushed while trying to learn it. I did play it on the easy difficulty, but that gave me a chance to make some mistakes during my first play-through.
I can't wait to play on the normal setting, and probably on a bigger map.
One thing that I noticed in the design of the game is that, even if one isn't going for a given type of victory, it still behooves one to progress that area, so nothing gets abandoned. For instance, even if one isn't going for domination victory, it's still a good idea to have a strong enough standing army to defend against invaders. Likewise, Culture is useful both to make someone else's Culture Victory harder and because it unlocks special abilities.
It's a short review, I know, but if you want an in-depth look at the mechanics - well, it's been out since 2010, so I'm sure that you can find reviews and wikis on it.
I've finally finished my first game of it.
I really quite enjoyed the game. There's a lot to it, but because of the way that civilizations progress, it's not all dumped out at once. Also, it's turn-based, so I'm not rushed while trying to learn it. I did play it on the easy difficulty, but that gave me a chance to make some mistakes during my first play-through.
I can't wait to play on the normal setting, and probably on a bigger map.
One thing that I noticed in the design of the game is that, even if one isn't going for a given type of victory, it still behooves one to progress that area, so nothing gets abandoned. For instance, even if one isn't going for domination victory, it's still a good idea to have a strong enough standing army to defend against invaders. Likewise, Culture is useful both to make someone else's Culture Victory harder and because it unlocks special abilities.
It's a short review, I know, but if you want an in-depth look at the mechanics - well, it's been out since 2010, so I'm sure that you can find reviews and wikis on it.
Friday, January 30, 2015
On the Average Results of Savage Worlds Dice
Something occurred to me the other day, regarding the average results of dice in Savage Worlds. For those who don't know, in Savage Worlds, each die (with the possible exception of damage dice - I forget) can explode. For those who don't know what that means, if a die rolls its highest result, that result is kept and then added to a new roll of that die.
Obviously, the minimum result of any roll (except 1d4-2) is a 1, and the maximum result is an arbitrarily large number. However, what's the average result of any die roll?
Consider a 1d6 roll, the most common roll in Savage Worlds.
Let x be the average result, which we seek.
}{6})
We're re-using x on the right, since the average roll being added to 6 in the best case is, itself, the average case of a new die roll. Thus, we can use basic algebra to solve for x:
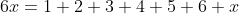
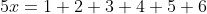
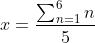
In this specific case, the result is x = 21/5 = 4.2. However, I've left the sum to reveal the generalized form. For a die of size k, the average result is
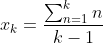
While I don't think that this is new knowledge, I also suspect that tables are commonly referenced, so I thought that I'd put this generalized form out there.
EDIT: I had a botched example result; I was thinking of the d8 case.
EDIT: I discovered that the fancy math stuff is rendering weirdly on Blogger. I'll fix it later; for now, you can click on it if it's illegible: The page where you land will have it (correctly) in about the middle.
Obviously, the minimum result of any roll (except 1d4-2) is a 1, and the maximum result is an arbitrarily large number. However, what's the average result of any die roll?
Consider a 1d6 roll, the most common roll in Savage Worlds.
Let x be the average result, which we seek.
We're re-using x on the right, since the average roll being added to 6 in the best case is, itself, the average case of a new die roll. Thus, we can use basic algebra to solve for x:
In this specific case, the result is x = 21/5 = 4.2. However, I've left the sum to reveal the generalized form. For a die of size k, the average result is
While I don't think that this is new knowledge, I also suspect that tables are commonly referenced, so I thought that I'd put this generalized form out there.
EDIT: I had a botched example result; I was thinking of the d8 case.
EDIT: I discovered that the fancy math stuff is rendering weirdly on Blogger. I'll fix it later; for now, you can click on it if it's illegible: The page where you land will have it (correctly) in about the middle.
Subscribe to:
Posts (Atom)