"Hey, Jerry," Benedict said, waving his friend over.
"Hey, what's up?" Jerry asked when he got there.
"Well, since the port's having some down time, we're swapping anecdotes about our home dimensions. This is Ken, by the way. Apparently, even though our dimensions are close to each other, the celebrities are wildly different. Like, um... Ooh, tell me about Michael Jackson."
"The musician?" Ken asked.
"No way!" Jerry interjected, "He stayed with music? We're talking Mad Michael Jackson, the pro wrestler, right? Well, no, I suppose not. But did yours start out in The Jackson 5, too?"
"Yeah, that's the one. He died of a drug overdose. Just as well, really."
"Oh yeah," added Benedict, "That's one thing: In both our dimensions, drug overdose is a really common way for celebrities to go."
"So your Michael Jackson was a pro wrestler?" asked Ken. "What about your Dwayne Johnson?"
"He was a pro wrestler, too," said Jerry, "but then he went on to sell these electric grills that drain fat into a catch basin."
"Oh, that was our George Foreman's schtick. Our Dwayne Johnson became an actor, but still started out in pro wrestling."
"Oh. We've basically got it the other way around: George Foreman went on to be an actor in B-grade sci-fi movies."
"Oh, weird," said Ken. "Let's see... Our Bob Ross was a painter, what was yours?"
"He did comic books back in the 20th century," said Benedict.
Just then, they all got alerts. Each saw that the other had just checked one, and correctly assumed that they were the same: The port was back to up time. They parted ways, and each left with the thought of how different-yet-similar things were between dimensions. Each was also glad that he wasn't a celebrity.
Sunday, November 30, 2014
Sudden Short Story 65
"I am told that you can free me," she said to the foreigner, as she sat by him in the tavern. Priestesses were uncommon there, but nobody would think to question her presence, either.
"If your will is bound by a deity, then yes, I can free you," he replied.
"And what do you seek in return?"
"I need access to the temple," he explained. "I also want me to tell me whatever you can about your highest priestess, as it will help me in my cause. Otherwise, I need little."
Hope stirred in her, that she might be able to escape her fate. "I must have something to call you, if I am to take you to the island. What is your name?"
"I have had many names, but I go by Asura-Anatakartta. It was given to me by a people from my home plane, after I slew the threefold god of the west."
The idea that he came from another plane of existence was very surprising to her, but she was trained to spot lies, and this man was not lying. "What brings you to our plane?"
"I have been exiled from my home plane. I do seek to return, but it is a long journey that I undertake."
"You slew a god, and you can free people from them. Who would want to exile you?"she asked.
"Other gods, of course. Deities think that they're untouchable until someone kills one and lives. Though, even that was not enough to warrant my exile, the first time. It was not until I slew Brahma that the rest of the Trimurti mustered enough power - theirs and their allies' - to banish me."
The priestess realized that she might be a bit out of her depth with this one, but there was still the mission to do, and she would be free. "Let us go, then," she said, standing. "Once I am free, perhaps I can help you on your journey home."
"You cannot, but thank you," he replied, as she led him out. She sensed that she should not ask further on that subject, and so she remained silent.
---
He waited outside of the high priestess's abode, just out of sight to anyone who would be leaving the doorway. The house servant was out on errands, so he had said that the house would need to be empty for his work to begin. He had not lied, but he had allowed her to believe that he would be doing a secretive investigation of the premises.
They were inside for a long time. The high priestess had sensed deception in her subordinate, but was unable to tease it out of her. Eventually, they left, headed toward a different part of the island. He crept up behind the high priestess, then ran her through the spine and heart with his sword.
"The thing about deities," he began. The young priestess spun around, startled that he had revealed himself, and then more startled at the dying body before her. "... is that most people don't really understand what they are, and each one is different. She didn't even realize it, but the high priestess was the goddess. I had uncovered that much during my previous investigation, before I even met you. And so, you are free," he said, wiping off his blade. "Unfortunately - and I am so very, very sorry for this part - she had already named you as her heir."
She was so shocked that, by the time that he charged at her, she was only able to throw up a simple shielding spell, which was immediately shattered on the point of a blade that had slain gods. She died free, but still she died.
"If your will is bound by a deity, then yes, I can free you," he replied.
"And what do you seek in return?"
"I need access to the temple," he explained. "I also want me to tell me whatever you can about your highest priestess, as it will help me in my cause. Otherwise, I need little."
Hope stirred in her, that she might be able to escape her fate. "I must have something to call you, if I am to take you to the island. What is your name?"
"I have had many names, but I go by Asura-Anatakartta. It was given to me by a people from my home plane, after I slew the threefold god of the west."
The idea that he came from another plane of existence was very surprising to her, but she was trained to spot lies, and this man was not lying. "What brings you to our plane?"
"I have been exiled from my home plane. I do seek to return, but it is a long journey that I undertake."
"You slew a god, and you can free people from them. Who would want to exile you?"she asked.
"Other gods, of course. Deities think that they're untouchable until someone kills one and lives. Though, even that was not enough to warrant my exile, the first time. It was not until I slew Brahma that the rest of the Trimurti mustered enough power - theirs and their allies' - to banish me."
The priestess realized that she might be a bit out of her depth with this one, but there was still the mission to do, and she would be free. "Let us go, then," she said, standing. "Once I am free, perhaps I can help you on your journey home."
"You cannot, but thank you," he replied, as she led him out. She sensed that she should not ask further on that subject, and so she remained silent.
---
He waited outside of the high priestess's abode, just out of sight to anyone who would be leaving the doorway. The house servant was out on errands, so he had said that the house would need to be empty for his work to begin. He had not lied, but he had allowed her to believe that he would be doing a secretive investigation of the premises.
They were inside for a long time. The high priestess had sensed deception in her subordinate, but was unable to tease it out of her. Eventually, they left, headed toward a different part of the island. He crept up behind the high priestess, then ran her through the spine and heart with his sword.
"The thing about deities," he began. The young priestess spun around, startled that he had revealed himself, and then more startled at the dying body before her. "... is that most people don't really understand what they are, and each one is different. She didn't even realize it, but the high priestess was the goddess. I had uncovered that much during my previous investigation, before I even met you. And so, you are free," he said, wiping off his blade. "Unfortunately - and I am so very, very sorry for this part - she had already named you as her heir."
She was so shocked that, by the time that he charged at her, she was only able to throw up a simple shielding spell, which was immediately shattered on the point of a blade that had slain gods. She died free, but still she died.
Saturday, November 29, 2014
Regarding Non-Alphabetical Ordering of Reduced Fractions as Strings
I ran across a programming problem a while back, and I've been meaning to post about the consequences of it. There is a situation in which there are fractions that are represented as strings and that, by default, sort alphabetically. The representations were immutable, but were usually reduced, so an ordering flag had to be added that would apply before the alphabetization. I'll try to describe the problem mathematically below.
Let F(n) be the set of fractions m/n such that m,n
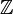, n > 1, n is not prime, 0 < m < n.
Note: If n were prime, then the solution would be trivial, since the fractions cannot be reduced, and therefore the proper order and alphabetical order would be the same.
Assume that either (1) we use a high enough base that n is always a single character, or (2) every string representation of the fraction m/n, for every value of m, is equally and sufficiently 0-padded in both the numerator and the denominator. (For an example of (2): If n=10, then 9/10 would be "09/10", and 8/10=4/5 would be "04/05".) For a given m, what is the minimum number of ordering flags such that, if each fraction m/n is associated with one, then sorted first by flag and then alphabetically, the fractions, even reduced, would be in ascending order?
An Example:
Let n = 8.
F(n) = {1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8} = {1/8, 1/4, 3/8, 1/2, 5/8, 3/4, 7/8}.
If sorted alphabetically, then these fractions would come out as "1/2, 1/4, 1/8, 3/4, 3/8, 5/8, 7/8".
Assume that 3 flags is sufficient. Call them "a", "b", and "c". Clearly, 1/8 will need "a", 1/4 will need "b", and 1/2 will need "c". Similarly, 3/4 will need either "a" or "b", and 3/8 will need either "b" or "c", but they cannot both take "b".
For brevity and clarity, I will simply tack the flag on the front of the fraction, so that alphabetical order will put them in the proper order. One valid association, then, produces "a1/8, b1/4, b3/8, c1/4, c5/8, c3/4, c7/8". (In fact, I just realized that this is the only valid association on 3 flags, but I'll leave this as an exercise.)
2 flags is not sufficient for this set: If any {1/2, 1/4}, {1/4, 1/8}, or {1/2, 1/8} get the same flag, then they will resolve in the wrong order.
When looking at the set, reduced, the minimum number of flags is at least the largest number of common numerators (3, in the above example, as 3 of the reduced fractions had 1 as their numerator). However, is there a good way to determine this purely from looking at n?
Note: I've also determined that 3 flags is sufficient when n=9, when n=10, and when n=6. Demonstration of this is left as an exercise.
Another example:
Let n = 4.
F(n) = {1/4, 2/4, 3/4} = {1/4, 1/2, 3/4}.
2 flags is sufficient: "a" must go with 1/4 and "b" with 1/2 (and 3/4), sorting them as "a1/4, b1/2, b3/4".
Note: In any case where 1 flag is sufficient, the solution is trivial. That is, flagging is unnecessary.
Conjecture: The minimum number of flags needed to sort the reduced fractions alphabetically is x, where x is one less than the number of factors (prime or otherwise) of n.
An example that attempts to exercise the conjecture:
Let n = 12.
Let H(n) be the set of factors of n. For n=12, H(12) = {1, 2, 3, 4, 6, 12}. The size of H is 6, so x=5.
F(12) = {1/12, 2/12, 3/12, 4/12, 5/12, 6/12, 7/12, 8/12, 9/12, 10/12, 11/12} = {1/12, 1/6, 1/4, 3/4, 5/12, 1/2, 7/12, 2/3, 3/4, 5/6, 11/12}.
This resolves as: "01/02, 01/03, 01/04, 01/06, 01/12, 02/03, 03/04, 05/06, 05/12, 07/12, 11/12".
Let us try to minimally alphabetize it:
a01/12, b01/06, c01/04, d01/03, d05/12, e01/02, e07/12, f02/03, f03/04, f05/06, f11/12.
5 flags was insufficient, as I had to go to 6 to put 2/3 after 7/12, so the conjecture is incorrect.
Well, that's all for now. I might revisit this problem at a later date. We'll see.
Let F(n) be the set of fractions m/n such that m,n
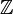, n > 1, n is not prime, 0 < m < n. Note: If n were prime, then the solution would be trivial, since the fractions cannot be reduced, and therefore the proper order and alphabetical order would be the same.
Assume that either (1) we use a high enough base that n is always a single character, or (2) every string representation of the fraction m/n, for every value of m, is equally and sufficiently 0-padded in both the numerator and the denominator. (For an example of (2): If n=10, then 9/10 would be "09/10", and 8/10=4/5 would be "04/05".) For a given m, what is the minimum number of ordering flags such that, if each fraction m/n is associated with one, then sorted first by flag and then alphabetically, the fractions, even reduced, would be in ascending order?
An Example:
Let n = 8.
F(n) = {1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8} = {1/8, 1/4, 3/8, 1/2, 5/8, 3/4, 7/8}.
If sorted alphabetically, then these fractions would come out as "1/2, 1/4, 1/8, 3/4, 3/8, 5/8, 7/8".
Assume that 3 flags is sufficient. Call them "a", "b", and "c". Clearly, 1/8 will need "a", 1/4 will need "b", and 1/2 will need "c". Similarly, 3/4 will need either "a" or "b", and 3/8 will need either "b" or "c", but they cannot both take "b".
For brevity and clarity, I will simply tack the flag on the front of the fraction, so that alphabetical order will put them in the proper order. One valid association, then, produces "a1/8, b1/4, b3/8, c1/4, c5/8, c3/4, c7/8". (In fact, I just realized that this is the only valid association on 3 flags, but I'll leave this as an exercise.)
2 flags is not sufficient for this set: If any {1/2, 1/4}, {1/4, 1/8}, or {1/2, 1/8} get the same flag, then they will resolve in the wrong order.
When looking at the set, reduced, the minimum number of flags is at least the largest number of common numerators (3, in the above example, as 3 of the reduced fractions had 1 as their numerator). However, is there a good way to determine this purely from looking at n?
Note: I've also determined that 3 flags is sufficient when n=9, when n=10, and when n=6. Demonstration of this is left as an exercise.
Another example:
Let n = 4.
F(n) = {1/4, 2/4, 3/4} = {1/4, 1/2, 3/4}.
2 flags is sufficient: "a" must go with 1/4 and "b" with 1/2 (and 3/4), sorting them as "a1/4, b1/2, b3/4".
Note: In any case where 1 flag is sufficient, the solution is trivial. That is, flagging is unnecessary.
Conjecture: The minimum number of flags needed to sort the reduced fractions alphabetically is x, where x is one less than the number of factors (prime or otherwise) of n.
An example that attempts to exercise the conjecture:
Let n = 12.
Let H(n) be the set of factors of n. For n=12, H(12) = {1, 2, 3, 4, 6, 12}. The size of H is 6, so x=5.
F(12) = {1/12, 2/12, 3/12, 4/12, 5/12, 6/12, 7/12, 8/12, 9/12, 10/12, 11/12} = {1/12, 1/6, 1/4, 3/4, 5/12, 1/2, 7/12, 2/3, 3/4, 5/6, 11/12}.
This resolves as: "01/02, 01/03, 01/04, 01/06, 01/12, 02/03, 03/04, 05/06, 05/12, 07/12, 11/12".
Let us try to minimally alphabetize it:
a01/12, b01/06, c01/04, d01/03, d05/12, e01/02, e07/12, f02/03, f03/04, f05/06, f11/12.
5 flags was insufficient, as I had to go to 6 to put 2/3 after 7/12, so the conjecture is incorrect.
Well, that's all for now. I might revisit this problem at a later date. We'll see.
Friday, November 28, 2014
Video Game Plans as of November 2014
Briefly, here's an update on video game stuff.
Though I got pokémon ORAS last week, I've only barely touched AS. I'm torn on time, though, since I still haven't finished my Gen I team in pokémon X, which I still intend to do, even if that's the last thing that I do in X. (I'm not expecting to do any special teams in AS, though.)
I'm planning to do a Y-Locke's Log this Sunday, since I never got to it before.
I'm also hoping to play some more FTL, which I haven't touched in a while, but that's probably going to get pushed back to December.
Also in December, I'm hoping to play through LEGO Indiana Jones, since it shouldn't take that long, and it should be simple to finish.
Anyway, it's looking like I've got to make a big video game push in the next few weeks. I'll let you know how it went, next month. ;)
Though I got pokémon ORAS last week, I've only barely touched AS. I'm torn on time, though, since I still haven't finished my Gen I team in pokémon X, which I still intend to do, even if that's the last thing that I do in X. (I'm not expecting to do any special teams in AS, though.)
I'm planning to do a Y-Locke's Log this Sunday, since I never got to it before.
I'm also hoping to play some more FTL, which I haven't touched in a while, but that's probably going to get pushed back to December.
Also in December, I'm hoping to play through LEGO Indiana Jones, since it shouldn't take that long, and it should be simple to finish.
Anyway, it's looking like I've got to make a big video game push in the next few weeks. I'll let you know how it went, next month. ;)
Tuesday, November 4, 2014
Y-Locke's Log: Day 8
Today had quite an interesting start to it indeed. I received a Diancie, but before I could even begin to get to know it, an anonymous butler and maid arrived, speaking of its remarkable beauty. But then, they asked me to give it to them! Fortunately, their master arrived to straighten the whole thing out. He also mentioned that rumor had it that Diancie is something of a good luck charm.
However, I had already committed to using Rose Red as my Fairy-type, so I put Diancie away, for now, and set back out on the road to train her up.
Rose Red isn't very tough yet, so I'm doing many bouts against wile pokémon; Theodore is her backup, for now. However, in one particularly tough fight against a Ledyba, I ended up switching Sly in, and, afterwards, he evolved into a Braixen!
The amount of training that I'm having to do to prepare Rose Red for battle reminds me of just how fragile some pokémon can be; she's fairly easily weakened, and I worry for the worst. Mousea is similarly weak, though I do at least get enough time to retrieve him for battle; he's not as frail, but he can barely damage anything, so, unfortunately, every battle using Mousea threatens to be a losing one.
Mousea did manage to learn Lucky Chant tonight, which should help her survive battles, since critical hits can do truly surprising amounts of damage. Theodore also learned Rollout. I look forward to a chance to try it out, but I've been training my pokémon all day, and I think that they could use a rest. ^_^
However, I had already committed to using Rose Red as my Fairy-type, so I put Diancie away, for now, and set back out on the road to train her up.
Rose Red isn't very tough yet, so I'm doing many bouts against wile pokémon; Theodore is her backup, for now. However, in one particularly tough fight against a Ledyba, I ended up switching Sly in, and, afterwards, he evolved into a Braixen!
The amount of training that I'm having to do to prepare Rose Red for battle reminds me of just how fragile some pokémon can be; she's fairly easily weakened, and I worry for the worst. Mousea is similarly weak, though I do at least get enough time to retrieve him for battle; he's not as frail, but he can barely damage anything, so, unfortunately, every battle using Mousea threatens to be a losing one.
Mousea did manage to learn Lucky Chant tonight, which should help her survive battles, since critical hits can do truly surprising amounts of damage. Theodore also learned Rollout. I look forward to a chance to try it out, but I've been training my pokémon all day, and I think that they could use a rest. ^_^
Subscribe to:
Posts (Atom)